サンプル TMD 同調質量ダンパー(TMD)制振建物
基本情報
建物概要
建物の最上部に錘を設置し、その揺れの周期を建物の固有周期に近い値にすることで、地震時の共振振動を低減させる仕組みを同調質量ダンパー(TMD: Tuned Mass Damper)という。
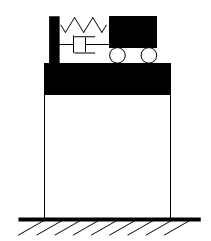
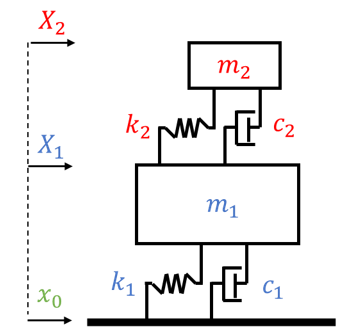
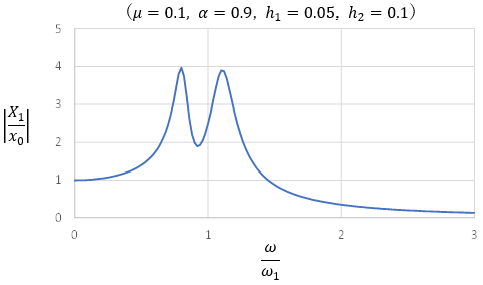
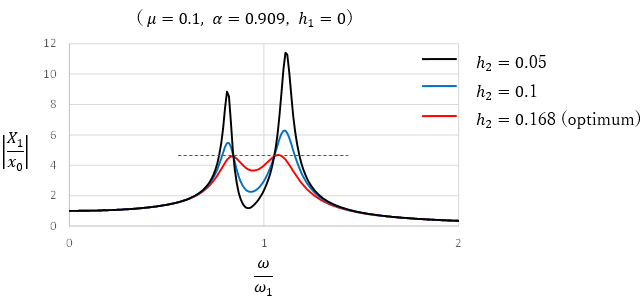
ここで、建物を主振動系(質量m1, 固有円振動数ω1,減衰定数h1)、TMDを従振動系(質量m2,固有円振動数ω2,減衰定数h2)とする。地動振幅x0の調和地動に対する主振動系の応答X1の比率(絶対応答倍率)を求めると以下の共振曲線が得られる。これより、主振動系の応答倍率は、振動数比1付近で共振曲線が谷となっており、その両側に2つの山ができている。なお、ここでは、質量比μ=m2/m1=0.1,振動数比α=ω2/ω1=0.9,主振動系の減衰定数h1=0.05,従振動数系の減衰定数h2=0.1としている。
主振動系の減衰定数h1=0のとき、TMDの減衰定数を変化させた共振曲線は、必ず同じ2点を通る。この点を定点といい、定点を利用して最適なTMDの振動数比と減衰定数を決定する手法を定点定理という。
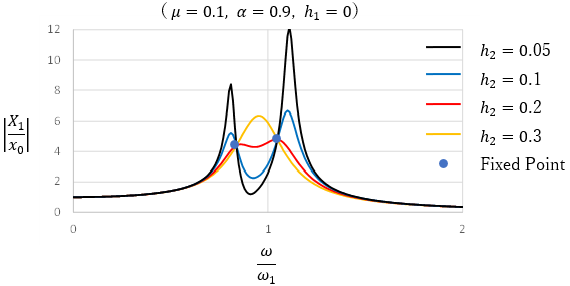
定点定理では、共振曲線の2つの極大値が同じになる振動数比を最適値として定める。さらに、定点が極大値となる減衰定数を最適値とする。これが最も応答場率が低減される最適同調された共振曲線となる。
定点定理から、最適振動数比は
![]()
最適減衰定数は
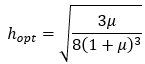
となる。式の誘導は、「TMDの基礎理論」にまとめてある。
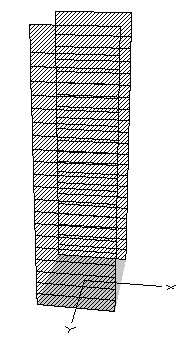
以下では、20階建ての超高層建物にTMDを設置した場合の例を示す。建物およびTMD(21層目)は、弾性せん断多質点系としてモデル化する。各層の弾性ばねと減衰(ダッシュポット要素)を別の要素と考え、それぞれの多質点系を並列に配置する。モデルの諸元や解析モデルの入力手順などは建物情報を参考にされたい。
データベース
建物情報には、モデルの諸元など、STERA_3Dの入力の元になった情報が含まれています。
| 建物情報 (*.pdf) | 入力ファイル (*.stera) | STERA_3D version | 著者 | 更新日時 | |
|---|---|---|---|---|---|
| 1 | B01_TMD_20F_J | 11.5 | Taiki Saito |
2024.07.21 |
解説

